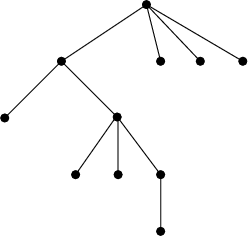
Figura 1. Un albero.
Un albero è formato da una radice e da un insieme finito e ordinato (eventualmente vuoto) di figli, che sono anch'essi alberi. Ad esempio, la Figura 1 rappresenta un albero: per convenzione, la radice viene disegnata in cima (cioè al contrario rispetto agli alberi veri). Come ogni albero, lo potete descrivere dicendo quanti figli ha la radice (in questo caso, quattro) e poi descrivendo uno a uno, nell'ordine da sinistra a destra, i quattro sottoalberi. In questo modo, ad esempio, l'albero in Figura 1 sarebbe identificato dalla seguente sequenza:
4 2 0 3 0 0 1 0 0 0 0

Infatti, l'albero ha quattro figli sotto la radice, per cui il primo numero è 4. D'altra parte, 2 0 3 0 0 1 0 è la descrizione del primo figlio, mentre gli ultimi tre figli sono ciascuno descritti da 0 (dato che non hanno figli).
Supponete di guardare l'albero riflesso in uno specchio. L'ordine dei figli di ciascun nodo risulta invertito. Per esempio, l'albero di Figura 1 appare come in Figura 2.
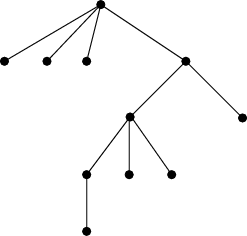
Questo nuovo albero è descritto dalla sequenza
4 0 0 0 2 3 1 0 0 0 0
fr = fopen( "input.txt", "r" ); fw = fopen( "output.txt", "w" );e in Pascal con un'istruzione tipo
assign( fr, 'input.txt' ); reset( fr ); assign( fw, 'output.txt' ); rewrite( fw );
File input.txt
4 2 0 3 0 0 1 0 0 0 0
File output.txt
4 0 0 0 2 3 1 0 0 0 0