TRAFFIC LIGHTS


SEMAFORI PROBLEMA Nella città di Dingilville il traffico è regolato in modo particolare: ci sono diversi incroci, e strade che si incontrano agli incroci. Fra due diversi incroci c'è sempre al massimo una strada, e non c'è alcuna strada che vada da un incrocio a se stesso. Il tempo di percorrenza di una strada è lo stesso in entrambe le direzioni. Ad ogni incrocio c'è un singolo semaforo che può essere blu o rosso in ciascun istante. I colori dei semafori si alternano periodicamente: blu per un certo periodo e rosso per un altro periodo. Un veicolo può transitare su una certa strada che collega due incroci se e solo se i semafori che si trovano ai due incroci hanno lo stesso colore nel momento il cui il veicolo parte da un'estremità per raggiungere l'altra. Se un veicolo arriva a un incrocio proprio nel momjento in cui il semaforo sta cambiando colore, si considera il colore nujovo. I veicoli possono aspettare agli incroci. Vi viene data una mappa della città che mostra i tempi di percorrenza per ciascuna strada (intero), le durate dei due colori per ciascun incrocio (interi) il colore iniziale del semaforo e il tempo residuo prima che cambi (intero) per ciascun incrocio. Il compito consiste nel trovare un percorso che necessiti il tempo minimo di percorrenza fra un dato incrocio (sorgente) e un dato altro incrocio (destinazione), considerato che il veicolo si trovi nella sorgente all'istante iniziale. Se esistono più cammini equivalenti, se ne deve riportare uno solo. ASSUNZIONI 2 <= N <=300 dove N è il numero degli incrocio. Gli incroci sono identificati da interi da 1 a N. Questi numeri vengono chiamati id. 1 <=M <=14,000 dove M è il numero di strade. 1 <= l_ij <= 100 dove l_ij è il tempo richiesto per spostarsi dall'incrocio i a j usando la strada che collega i a j. 1 <= t_ic <= 100 dove t_ic è la durata del colore c per il semaforo dell'incrocio i. L'indice c è B per il blu o P per il rosso (purple). 1 <= r_ic <= t_icdover_ic è il tempo residuo per il colore c all'incrocio i. 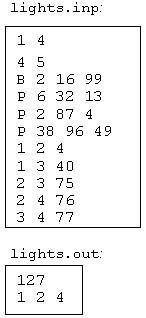INPUT L'input è contenuto nel file lights.inp. La prima riga contiene due numeri: L'id dell'incrocio sorgente e l'id dell'incrocio destinazione. La seconda riga contiene i due numeri N, M. Le seguenti N righe contiene informazioni sugli N incroci. La (i+2)-esima riga del file di input contiene informazioni sull'incrocio i : C_i, r_ic, t_iB, t_iP dove C_i può essere ‘B’ o ‘P’, ad indicare il colore iniziale del semaforo all'incrocio i. Le ultime M righe contengono informazioni sulle M strade. Ogni riga ha la seguente forma: i, j, l_ijdovei e j sono gli id degli incroci collegati da questa strada. OUTPUT L'output dovrà essere contenuto nel file lights.out. Se un cammino esiste: La prima riga conterrà il tempo richiesto dal cammino minimo che collega l'incrocio sorgente e l'incrocio destinazione. La seconda riga contiene la lista degli incroci che costituiscono il cammino minimo trovato. Gli id degli incroci sono scritti nel file di output nell'ordine in cui vengono percorsi. Quindi il primo intero della riga sarà l'id dell'incrocio sorgente e l'ultimo sarà l'id dell'incrocio destinazione. Se non esiste alcun cammino: Una singola riga che contiene solo il numero 0. ESEMPIO VALUTAZIONE Tempo massimo di esecuzione: 2 secondi. Nessun credito parziale. Soluzione Essenzialmente l'algoritmo di Dijkstra, con i valori dei pesi ricalcolati ad ogni iterato.

Soluzione