Problema: Gara automobilistica
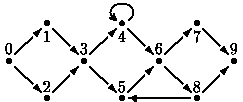
La figura 1 mostra un esempio di un circuito per una gara automobilistica.
Vedete alcuni punti, etichettati da 0 a N (qui N=9), e alcune
frecce che li connettono. Il punto 0 è l'inizio della gara; il punto
N
la fine. Le frecce rappresentano strade a senso unico. I partecipanti alla
gara si spostano da punto a punto attraverso le strade, e possono farlo
solo nella direzione delle frecce. A ogni punto un partecipante può
scegliere di proseguire su qualunque freccia uscente.
Figura 1: Un circuito automobilistico con 10 punti
Un circuito ben formato ha le seguenti proprietà:
-
Ogni punto del circuito può essere raggiunto dall'inizio;
-
La fine può essere raggiunta da qualunque punto del circuito;
-
La fine non ha frecce uscenti.
Un partecipante non deve passare necessariamente per ogni punto del circuito
per raggiungere la fine. Ciononostante, alcuni punti sono inevitabili.
Nell'esempio, sono i punti 0, 3, 6 e 9. Dato un circuito ben formato, il
vostro programma deve determinare l'insieme dei punti inevitabili che tutti
i partecipanti devono visitare, esclusi inizio e fine (sottoproblema A).
Supponiamo che la gara debba essere tenuta in due giorni consecutivi.
A questo scopo il circuito deve essere diviso in due circuiti, uno per
ogni giorno. Il primo giorno, l'inizio è nel punto zero, e la fine
in qualche "punto di spezzamento". Il secondo giorno, l'inizio è
nel suddetto punto di spezzamento e la fine è nel punto N.
Dato un circuito ben formato, il vostro programma deve determinare l'insieme
dei punti di spezzamento (sottoproblema B). Un punto S è
di spezzamento per il circuito ben formato C se S non è
l'inizio o la fine di C, e il circuito può essere spezzato
in due circuiti ben formati che non hanno frecce comuni e hanno S
come solo punto comune. Nell'esempio, il solo punto di spezzamento è
3.
Dati in input
Il file INPUT.TXT descrive un circuito ben formato con al più
50 punti e al più 100 frecce. Ci sono N+1 righe nel file.
Le prime N righe contengono i punti finali delle frecce che escono dai
punti da 0 a N-1, rispettivamente. Ognuna di queste righe termina
con il numero -2. L'ultima riga contiene il numero -1.
Dati in output
Il vostro programma deve scrivere due righe nel file OUTPUT.TXT.
La prima riga deve contenere il numero di punti inevitabili nel circuito
in input, seguito dalle etichette dei suddetti punti, in qualunque ordine
(sottoproblema A). La seconda riga deve contenere il numero di punti di
spezzamento del circuito in input, seguito dalle etichette dei suddetti
punti, in qualunque ordine (sottoproblema B).
Esempio di input e output
La figura 2 mostra un input e un ouput possibili per l'esempio dato in
figura 1.
_____________ ______________
| INPUT.TXT | | OUTPUT.TXT |
|___________| |____________|
| 1 2 -2 | | 2 3 6 |
| 3 -2 | | 1 3 |
| 3 -2 | |____________|
| 5 4 -2 |
| 6 4 -2 |
| 6 -2 |
| 7 8 -2 |
| 9 -2 |
| 5 9 -2 |
| -1 |
|___________|
Figura 2: Esempio di input e output